Entropy Everywhere
Entropy in my life
This post was suppose to be the second part in a multi-part series about the heat equation as an example in high performance computing (HPC), unfortunately, Hurricane Ida had other plans and her strength is greater than my ability to power and remotely access Tulane’s computing cluster, Cypress. As of the time that I’m writing this, it is a little over a week since Ida felt like I had too much internet access and ability to power my laptop and decided to wreck havoc across the country. Hurricanes, for whatever reason, have decided to co-opt vocabulary related to statistical mechanics. Variations, ensemble models and uncertainty. While in statistical mechanics we have a chance to address uncertainty or, at least, understand it as best we can, in life it’s not so easy. If any of my blog has helped you (maybe a homework problem) or you have a soft spot in your heart for college students please donate to the Tulane University Student Emergency Aid and Assistance Fund and help make things a little easier, and a little more certain. For many students, especially international students, help from FEMA, or renters insurance, can be hard to come by so this becomes one of few ways that students can get help.
I was on vacation in Austin when I learned about Ida’s potential path and that people in New Orleans were preparing for evacuation. While I was, in a way, evacuated, the timing left much to be desired and had unwittingly jumped the gun. Unable to grab the necessities for an evacuation myself (not a lot of overlap in things that I pack for vacation and necessities for an evacuation) I was at the mercy of uncertainty. Fortunately, through the help of loved ones (shoutout Julia), and a couple of lucky breaks we were able to evacuate safely.
Fuck Ida, hurricanes suck.
While Ida threw a wrench in my HPC blog plans it gave me a lot of time to think about uncertainty. My plan on when to defend my thesis? Uncertain. What will I do when I graduate? Uncertain. Will I finish last in my fantasy football league after drafting J.K. Dobbins? Uncertain. But I’m not uncertain about uncertainty.
What is entropy?
The best explanation of entropy that I’ve read is E.T. Jaynes‘ famous paper Where Do We Stand on Maximum Entropy. If you like drinking water from a firehose, I suggest reading it. If you don’t, entropy is a quantitative measure of uncertainty. This should be no surprise since Gibbs/Shannon entropy formula,
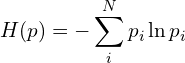
Requires probabilities, a way for us to assign the likelihood of an “uncertain” outcome. Maximizing entropy with probability (uncertainty) constraints, Maximum Entropy (MaxEnt) finds the least committal statistical inference when incomplete information is present. Least committal means that MaxEnt is producing a probability distribution that is independent of subjectivity or opinion of a particular person. Taking in only well established information from the macrostate and using that as a constraint in maximizing the entropy.
MaxEnt is very important and its effectiveness can be shown in a simple problem.
Brandeis dice problem
Jaynes invented the Brandeis Dice Problem as a simple illustration of MaxEnt. The problem:
A die has been tossed a very large number N of times, and we are told that the average number of spots per toss was not 3.5, as we might expect from an honest die, but 4.5. Translate this information into a probability assignment Pn, n = 1, 2, . . . , 6, for the n-th face to come up on the next toss.
Because all we know is information about the macrostate, i.e. that the ![]() , where
, where ![]() is the roll of a die. MaxEnt provides a way to produce probability distributions by maximizing the entropy.
is the roll of a die. MaxEnt provides a way to produce probability distributions by maximizing the entropy.
(1) 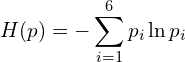
(2) 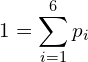
(3) 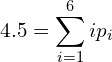
Combining Eq. (1), Eq. (2) and Eq. (3) forming the Lagrangian,
(4) 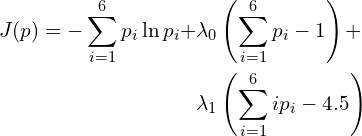
Taking the derivative of ![]() and setting to zero,
and setting to zero,
![]()
(5) ![]()
We can divide ![]() by 1 resulting in,
by 1 resulting in,
(6) 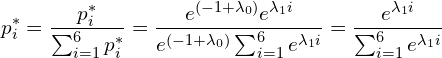
We can now solve the equation,
(7) 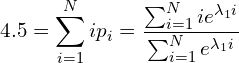
Here let ![]() , Eq. (7) now becomes,
, Eq. (7) now becomes,
(8) 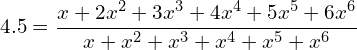
Here ![]() . The resulting probabilities are,
. The resulting probabilities are,

![Rendered by QuickLaTeX.com E[X] = 4.5](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-d5d39b8924530ee449c0dc8848436049_l3.png) .
.MaxEnt provides an easy and straight forward way to solve for the distribution of probabilities knowing only characteristics of the macrostate, the expected value of a roll. While this problem is simple (relatively) to solve, below I have provided some R code to solve it!